명제 논리
명제
먼저 명제라는 것은 참, 거짓을 분명하게 판정할 수 있는 문장들을 명제라 하고 예를들어 1+1=3 은 거짓인 명제이며 나의 이름은 코코팡이다 라는 문장은 참인 명제이다. 하지만 일어나서 아침을 먹자 와 같이 참과 거짓을 나눌 수 없는 문장은 명제라 할 수 없다.
보통 명제를 표현할 땐 p,q등과 같이 표현하며 실직적으로 명제는 문장자체의 내용에 대해선 무관심하며 참이냐 거짓이냐에 포커스를 둔다.
명제에는 기본 명제와 복합명제가 있다.
기본 명제는 하나의 진술로 이루어진 최소 단위의 명제이고
복합 명제는 기본 명제들이 겹합이 된 명제이다.

단일로 존재하는 P와Q가 기본 명제이며 이를 결합한 P^Q가 복합 명제이다.
논리식
명제를 기호로 표현한 형식이며 명제기호,참과 거짓을 나타내는 T와F, 명제 기호를 연결하는 논리 기호로 구성한다.

명제 논리나 술어 논리에 자주 등장하는 용어들이 있다.
1. 리터럴(literal)
명제 기호P 자체이거나 명제 기호의 부정한 것을 말한다.
2.절(clause)
리터럴들이 논리합으로만 연결되있는 것들
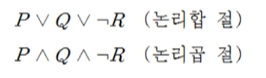
이렇게 연결이 되어있으면 절이라고 하지만 괄호안에 논리합, 논리곱이 없이 그냥 절이라고 표현이 되어있으면 "논리합 절" 이라고 생각하면 된다.
3. 논리곱 정규형(CNF)
논리합 절들이 논리곱으로 연결되어 있는 논리식이다.

4. 논리합 정규형(DNF)
논리곱 절들이 논리합으로 연결되어 있는 논리식이다.

정형식
앞에서 본 논리식만으로 구성을 하면 제대로 된 논리식이 된다고는 보장을 못한다. 예를들어 자연어에서 우리가 아무렇게나 배치를 한다고 해서 제대로된 문장이 되는게 아니기에 논리도 그 구성요소들을 어떻게 배치를 하냐에 따라 달라진다.
이를 정형식을 가지고 문법에 맞는 논리식을 만들어 주는 식이다.
예를들어

그리고 단일 명제와 복합 명제에 대한 값을논리기호에 따라 나타낼 수 있는데 이르 진리표를 가지고 표현이 가능하다.

그리고 이렇게 진리표를 참고하여 논리식을 해석할 수 있다.
1.논리식의 해석
논리식의 명제기호에 T AND F 를 할당을 해야한다.
EX)
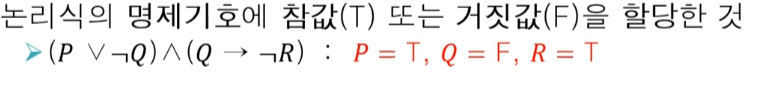
이렇게 명제기호에 값을 할당하는 것을 해석이라 한다.
위에 그림처럼 해석을 주었으면 진리표를 사용하여 논리식의 진리값을 결정할 수 있다.
그리고 N개의 명제기호가 논리식에서 사용이 된다라고 했을 때 각각T또는 F의 값을 가질 수 있기 때문에 총

의 해석을 가질 수 있다.
타당한 논리식
어떠한 해석에 대해서 항상 참(T)인 논리식을 타당한 논리식이라고 하며 다른 용어로써는 항진식이라 한다.
EX)

그렇다면 이와 반대인 개념도 존재한다. 이름은 항위식이며 어떠한 해석에 대해 항상 거짓이 되는 논리식이다.
EX)

충족가능한 논리식
참으로 만들 수 있는 해석이 하나라도 있는 그러니까 거짓과 참으로 조합이 된 논리식 이더라도 결론이 참인 논리식이다.
EX)

충족불가능한 논리식
참으로 만들 수 있는 해석이 전혀 없는 논리식이다.

동치관계의 논리식
어떠한 해석에 대해서도 같은 진리값을 갖는 두 논리식이다.
EX)

동치관계를 이용한 논리식의 변환
논리식의 동치관계를 이용하면 임의의 논리식을 논리곱 정규형(CNF)과 같은 정형식을 변환할 수 있다.
